A Modified Importance-Performance Framework for Evaluating Recreation-Based Experiential Learning Programs

Introduction

Recreation-based experiential learning is a valuable tool that can be used to further the goals of Extension programs and practitioners. At the core of the 4-H philosophy is the idea that individuals learn by doing (National 4-H Headquarters, n.d.). Experiential learning is a natural extension of this philosophy and involves applying old and new knowledge to novel situations (Torock, 2009). A commonality between Extension programming and experiential learning is that all experience matters, although not all experiences are equally educative (Dewey, 1938; Enfield, Schmitt-McQuitty, & Smith, 2007). Rigorous program evaluation helps ensure that knowledge transfer, and ultimately behavior change, are occurring in accordance with program design. Evaluation is therefore a necessary step in the programming cycle and a means of demonstrating value to stakeholder groups (Stup, 2003). This article illustrates a simple method of evaluating recreation-based experiential learning programming through the use of a modified importance-performance analysis (IPA) framework. Data are drawn from a university recreation-based experiential learning course containing both a classroom component and a field component.

IPA Framework

IPA is a method of evaluating and improving service quality (Martilla & James, 1977). The comparative simplicity of IPA with regard to both data analysis and application make it an attractive method for Extension practitioners and evaluators. Conducting an IPA is a three-step process:

1. A set of important attributes of the service being evaluated is compiled (in our example, course objectives from the syllabus).
2. In a pre-experience survey, respondents rate the importance of each attribute on a scale of 1 to 5 (1 = not at all important, 5 = very important); in a post-experience survey, respondents rate the performance of each attribute on a scale of 1 to 5 (1 = very poor, 5 = excellent).
3. Attributes are plotted on a two-dimensional matrix on the basis of their mean importance and performance scores (see Figure 1).

Figure 1.
Traditional Importance-Performance Analysis Matrix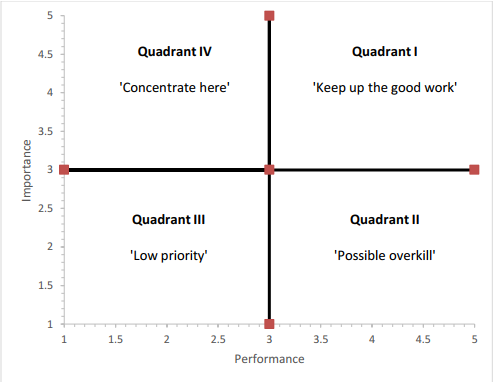

Adapted from "Importance-Performance Analysis," by J. A. Martilla and J. C. James, 1977, Journal of Marketing, 41(1), pp. 77–79.

When attributes are plotted on the matrix, each attribute falls into one of four quadrants. The upper right quadrant contains items rated as having high importance and high performance, signifying an evaluation that essentially means "keep up the good work." The lower right quadrant contains items rated as having low importance but high performance, suggesting that there may be overkill associated with these items. The lower left quadrant contains items rated as having low importance and low performance, suggesting that a low priority should be placed on these items. Finally, the upper left quadrant contains items rated as having high importance and low performance, implying that efforts should be concentrated on these items. Items that fall into the "concentrate here" quadrant are of greatest interest to evaluators, as they represent areas for potential improvement.

Modifications for Recreation-Based Experiential Learning

Two modifications are necessary to improve the applicability of IPA to recreation-based experiential learning. Because satisfaction is often very high for recreational experiences (Manning, 2010), attributes tend to cluster in the "keep up the good work" quadrant, providing little useful information to evaluators. A reorganization of the matrix addresses this issue (Abalo, Varela, & Manzano, 2007) and is illustrated in Figure 2. On the reorganized matrix, any item with an importance score higher than its performance score falls in the "concentrate here" quadrant.

Figure 2.
Modified Importance-Performance Analysis Matrix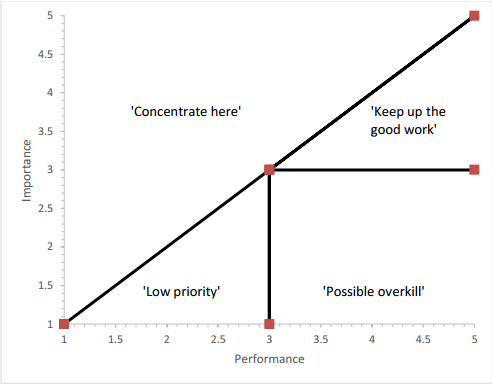

Adapted from "Importance Values for Importance-Performance Analysis: A Formula for Spreading Out Values Derived from Preference Rankings," by J. Abalo, J. Varela, and V. Manzano, 2007, Journal of Business Research, 60(2), 115–121.

The second modification involves including standard deviations for importance and performance scores, thereby addressing concerns about validity of the method when applied to small samples (Guadagnolo, 1985; Tarrant & Smith, 2002) and providing more nuanced information to evaluators. This modification is achieved through the inclusion of standard deviation error bars as part of the data presented on the reorganized matrix.

Application of Modified IPA

To demonstrate the application of this tool, we used both the traditional and modified IPA frameworks to analyze data from a university recreation-based experiential learning course. The course consisted of nine classroom meetings, followed by a week-long stay in a national park. The main focus of the course was to provide practical, hands-on experience for natural resource management and outdoor recreation students interested in park management. Data were collected through the use of pre- and post-experience surveys (N = 46) administered online via Qualtrics. Although 16 attributes based on course objectives were measured, we address only three in the example provided here. Data used in the example are summarized in Table 1.

Table 1.
Data Used in Importance-Performance Analysis Example

Attribute	Importance M	Performance M	Importance SD	Performance SD
Demonstrating the management of a national park	4.56	4.15	.629	.667
Applying classroom knowledge to the field	4.05	4.35	.834	.821
Networking with non-park professionals	3.55	4.18	1.109	.904

Initially, we used the traditional IPA framework to plot the three attributes on the four-quadrant grid (Figure 3). Because all three attributes clustered in the upper right "keep up the good work" quadrant, no information useful to evaluators was provided (this same pattern was also observed for the additional 13 attributes measured in the larger study).

Figure 3.
Results from Use of the Traditional Importance-Performance Analysis Framework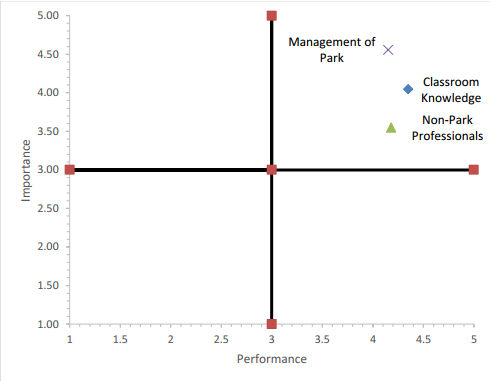

Next, we plotted the same data points on the reorganized grid and included standard deviations (Figure 4). On the reorganized grid, one of the three attributes was in the "concentrate here" quadrant (above the diagonal line), and the other two remained in the "keep up the good work" quadrant. The results of the modified analysis indicated that the program is effectively providing opportunities to network with non-park professionals and apply classroom knowledge to the field but that resources may need to be allocated to improving delivery of the attribute demonstrating the management of a national park.

The addition of standard deviation error bars showed that (a) none of the attributes fall cleanly into a single quadrant and (b) levels of agreement regarding importance and performance vary across the attributes. For example, there appears to be greatest crystallization around demonstrating the management of a national park and least concurrence regarding networking with non-park professionals. Such variation may indicate inconsistency in the delivery of certain attributes and illustrates that although an attribute may be performed to the satisfaction of most participants, there is variability among responses.

Figure 4.
Results from Use of the Modified Importance-Performance Analysis Framework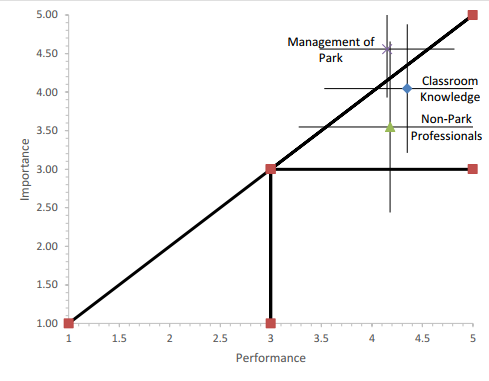

Conclusion

Information provided through use of the modified IPA framework can help guide the efforts of evaluators and programmers. Programmers may use the relative positions of attributes on the modified grid to identify areas of potential improvement and to make decisions regarding the allocation of resources. The relative lengths of the standard deviation error bars provide information regarding levels of agreement about the importance and performance of each attribute and indicate whether an attribute falls squarely into a single quadrant or crosses borders. For program evaluators, the modified IPA framework illustrated here can provide more nuanced information about overall program performance that may be useful in making decisions regarding the continuation or elimination of recreation-based experiential learning programs.

References

Abalo, J., Varela, J., & Manzano, V. (2007). Importance values for importance-performance analysis: A formula for spreading out values derived from preference rankings. Journal of Business Research, 60(2), 115–121.

Dewey, J. (1938). Experience and education. New York, NY: The Macmillan Company.

Enfield, R. P., Schmitt-McQuitty, L., & Smith, M. H. (2007). The development and evaluation of experiential learning workshops for 4-H volunteers. Journal of Extension, 45(1) Article 1FEA2. Available at: www.joe.org/joe/2007february/a2.php

Guadagnolo, F. (1985). The importance-performance analysis: An evaluation and marketing tool. Journal of Park and Recreation Administration, 3(2), 13–22.

Manning, R. E. (2010). Studies in outdoor recreation. Corvallis, OR: Oregon State University Press.

Martilla, J. A., & James, J. C. (1977). Importance-performance analysis. Journal of Marketing, 41(1), 77–79.

National 4-H Headquarters. (n.d.). 4-H programs at a glance. Retrieved June 28, 2016, from: http://4-h.org/parents/programs-at-a-glance/

Stup, R. (2003). Program evaluation: Use it to demonstrate value to potential clients. Journal of Extension, 41(4) Article 4COM1. Available at: www.joe.org/joe/2003august/comm1.php

Tarrant, M. A., & Smith, E. K. (2002). The use of a modified importance-performance framework to examine visitor satisfaction with attributes of outdoor recreation settings. Managing Leisure, 7(2), 69–82.

Torock, J. (2009). Experiential learning and Cooperative Extension: Partners in non-formal education for a century and beyond. Journal of Extension, 47(6) Article 6TOT2. Available at: www.joe.org/joe/2009december/tt2.php