The Need for Accurate Prediction Equations for the Carcass Lean Content of Pigs

Introduction

Prediction equations for carcass lean mass and lean percentage are widely used by commercial pork producers, and in teaching, research, and Extension. Researchers use carcass measurements in published equations to estimate the fat-free lean (FFL) content of pigs of different experimental treatments or genetic populations because the level of dissection and chemical analyses required to determine actual pork carcass fat-free lean content is too expensive for most swine research trials. The fat-free lean content is a critical measurement used to compare animals, estimate nutrient requirements, and as a measure of carcass merit by youth in livestock judging contests.

Fat-free lean gain is a measure of carcass muscle growth that is used to estimate daily lysine and essential amino acid requirements in the NRC (1998) and swine Extension nutrition guides (Von Heugten, 2009). Pork producers understand that producing pigs with excessive fat is inefficient and unprofitable (Keeler, Tokach, Goodband, Nelssen, & Langemeier, 1994). Uniform prediction of carcass leanness is needed to provide the technical information necessary for producers to implement genetic, nutritional, or management changes (Keeler et al., 1994).

Prediction equations are also used in teaching to describe the relationships amongst carcass or live animal measurements and carcass leanness. Undergraduate animal evaluation courses and competitive animal evaluation contests use prediction equations to estimate percent lean in pork carcasses.

Evaluation of live animal and carcass composition is a key aspect of any 4-H livestock project (Nash, 2007). The backfat thickness and degree of muscling (loin muscle area or depth) are either measured or visually evaluated. Pigs are measured by either carcass evaluation or real time ultrasound (Nash, 2007) in many swine shows. The relationships of percent carcass lean to these measurements established by the prediction equations are used to estimate differences in the relative leanness of different pigs or sets of pigs.

If the prediction equations are wrong, incorrect or inaccurate relationships between the physical measurements and carcass leanness will be used, and the placing of pigs with different relative carcass composition may not be correct. This can cause conflict, particularly in 4-H youth shows, where learning decision-making skills and the ability to defend a decision are critical components of the learning process (Rusk, Martin, Talbert, & Balschwied, 2002). The placing of pigs in livestock judging contests involves the weighting of perceived leanness, growth rate, structural soundness and other physical attributes (Rusk et al., 2002). The correct placing of pigs is not possible if the persons involved do not correctly evaluate differences in carcass composition.

The users of prediction equations assume that the equations are accurate, that they account for a high percentage of the actual variation in percent lean between pigs, and that they can be used to accurately estimate the differences between pigs of different treatments or genetic populations. The use of inaccurate equations can result in incorrect research results and conclusions.

Current Prediction Equations

There are two sets of the fat-free lean equations that are currently being widely used in the pork industry. The newer equations published in the Journal of Animal Science (Johnson, Berg, Goodwin, Mabry, Miller, Robison, Sellers, & Tokach, 2004) include data from the quality lean growth modeling (QLGM) trial (n = 627 pigs) and three other trials (n = 397) conducted by the National Pork Board (NPB). These equations will be referred to as the "2004 equations." These equations were designed to replace the equations in the Pork Composition and Quality Assessment Procedures (NPB, 2000, Burson, 2001), which only used data from the QLGM trial. The pigs had a mean backfat depth of 1.08 inches with a standard deviation of 0.33 inches and a range of 0.3 to 2.3 inches of backfat depth. These equations will be referred to as the "2000 equations."

Currently, the majority of U.S. pork processors use either carcass ultrasound or optical probe measurements of backfat depth and loin depth to predict carcass lean composition and carcass value. The predicted percent fat-free lean (FFL%) at 220 lb. of carcass weight from equations predicting FFL mass (FFLM) or FFL% using the 2004 equations are shown (Figure 1) for the Animal Ultrasound (AUS), fat-o-meter (FOM), and ultrasonic FOM (UFOM), which measure loin and fat depth. A 0.03 inch reduction in loin depth was predicted for each 0.10 inch increase in fat depth. The AUS equation for FFLM predicted that FFL% decreased as backfat increased to a minimum of 45.2% at 1.61 inches of backfat depth. Above 1.61 inches of backfat depth, the AUS equation for FFLM predicted FFL% increased as backfat depth increased. The AUS equation for FFL% predicted that FFL% decreased from 47.7% at 1.06 inches of backfat depth to 45.95% at 1.57 inches of backfat and then increased back to 47.7% at 2.04 inches backfat depth.

Figure 1.
Predicted Percent Fat-Free Lean Using Prediction Equations of Johnson et al. (2004) at 220 Pounds of Carcass Weight

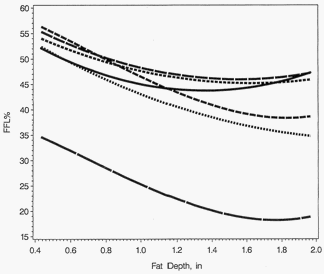
Note: The equations either predict fat-free lean mass (FFLM) or fat-free lean percentage (FFL%). A 0.30 mm decrease in loin depth was predicted for each 1 mm increase in backfat depth.

The UFOM equation for FFLM predicted that pigs achieved a minimal FFL% of 43.7% at 1.34 inches of backfat. Pigs with 1.0 and 1.73 inches of backfat depth are predicted to have 45% FFL. Pigs with 0.71 and 2.10 inches of backfat were predicted to have 49% from the equation for FFLM. The FOM equations for FFL% and FFLM are different from each other by 21 percentage units and have different curvilinear relationships relative to backfat depth than from the other equations. Obviously, pigs with such drastically different backfat depths do not have the same FFL% that the 2004 equations predict.

The accuracy of equations is best evaluated by the residual standard deviation (RSD) for FFL%. A lower RSD value indicates greater accuracy of the equation (European Community, 1994; Fortin, Tong, & Robison, 2004; Pomar, Marcoux, Gispert, Furnols, & Daumas, 2008). The 2004 equations had RSDs for FFL% from 3.74 to 4.23% for either ultrasonic or optical probe measurements of backfat and loin depth (Johnson et al., 2004), which is generally considered too high (EC, 1994). The total standard deviation for FFL% was approximately 5% (Johnson et al., 2004). These equations account for only 28 to 44% of the total variance in FFL%.

Using the 2004 equations, pigs with drastically different backfat depth can have the same predicted FFL%. Also, the same set of pigs has drastically different predicted FFL% depending on which prediction equation is used. The estimated difference in FFL % between two sets of pigs is drastically different depending on which instrument and which equation is used.

Swine researchers and educators tend to use fat-free lean prediction equations that include carcass weight, tenth rib backfat depth, and loin muscle area. The RSD for the equation, including ribbed carcass measurements, in Johnson et al. (2004) had an RSD of 3.12%. Recently, researchers calculated RSDs of 2.0 to 2.3% in the prediction for FFL% from ribbed carcass measurements (Schinckel, Wagner, Forrest, & Einstein, 2010, Table 2). The lower values indicate that these equations are more accurate. These equations accounted for 95% of the actual variation in FFL% between the seven genetic populations evaluated in the trial. The correlation between the true and predicted genetic population means for FFL% was 0.94. These equations accurately predict the actual genetic population means and differences between the genetic populations.

Equation Inconsistencies and Prediction Biases

The current NPB-AMSA equations in use in the United States (NPB, 2000; Burson, 2001) only include linear carcass measurements and only data from the QLGM trial. By only including linear variables, the RSDs for these equations are actually greater than the RSDs of equations, which include all significant linear-quadratic terms. The accuracies (RSDs for FFL%) of these equations were not provided with the 2000 equations, nor were the magnitude of the genetic line biases. Yet these equations have been widely used in Extension, research, and teaching for the past 11 years.

The least-squares means for lipid-free soft tissue mass were provided for the QLGM trial (NPB, 1999, Table 1). The values were adjusted for the linear carcass measurements included in the prediction equation. These least-squares means for each line are actually the overall mean of 114.9 lbs. plus the prediction bias: the under- or over- estimation for each line. The least squares mean for each line is the lipid-free soft tissue mass adjusted to the overall mean carcass measurements. The difference between each line's least-squares mean minus the overall mean is an estimate to what extent the prediction equation over or under predicts the actual mean for each genetic line of pigs. Pigs from genetic line 1 had 106.2 lbs. of lipid-free soft tissue adjusted for last rib backfat and pigs from line 2 had 120.5 lbs. Thus, the lipid-free mass of line 1 pigs is overestimated by 8.7 lbs. (106.2 – 114.9) and the lipid-free mass of line 2 pigs is underestimated by 5.6 lbs (120.5-114.9). The actual difference in lipid-free mass between pigs from lines 1 and 2 is actually 14.3 lbs. (8.7 + 5.6) greater than predicted from the last rib carcass measurements.

Table 1.
Least-Squares Means for Lipid-Free Soft Tissue Mass for Two Lines of Pigs (lbs.)¹

	Last rib ruler	Fat-o-meter	AUS2	Carcass3	Scan4
Line 1	106.2	110.4	103.8	111.5	110.2
Line 2	120.5	117.9	119.4	117.8	119.3
1 Model includes linear effects of the carcass measurements from NPB (1999). 2 Animal Ultrasound Systems 3 Carcass, 10th rib backfat depth and loin muscle area. 4 Real-time live animal fat depth and loin muscle area scan.

For the FOM, the lipid-free mass of line 1 pigs was overestimated by 4.5 lbs. The lipid-free mass of line 2 pigs was under predicted by 3.2 lbs by the FOM. The actual difference between the two genetic lines was 7.5 lbs. greater than predicted by the FOM equation. The AUS over predicted the lipid-free mass of line 1 pigs by 11.1 lbs. and under predicted the lipid-free mass of line 2 pigs by 4.5 lbs. Thus, the actual difference in lipid-free mass between the two lines was 15.6 lbs. greater than predicted by the AUS equation. The carcass measurements over predicted the lipid-free mass of line 1 pigs by 3.4 lbs. and under predicted the lipid-free mass of line 2 pigs by 2.9 lbs. The actual difference between the two lines for lipid-free mass was 6.3 lbs. greater than predicted.

The actual difference between the genetic lines was about 20 lbs. of lipid-free soft tissue based on the genetic line differences in backfat and loin muscle area. Thus, the last rib ruler, the FOM, the AUS, carcass, and live animal real time predicted about 28.3, 62.9, 22.0, 68.5, and 54.5% of the actual difference between pigs from genetic lines 1 and 2. These equations sometimes predict as little as 8% and only predict 47% at best, of the actual variation in lipid-free soft tissue percentage between the genetic lines. Equations should account for 90% of the variation between genetic populations or treatments to be used in research and modeling of nutritional requirements (Schinckel & de Lange, 1996).

Concerns with the Prediction of Lean Gain

The genetic line differences and prediction biases for fat-free lean are greater than for lipid-free soft tissue (Schinckel, Wagner, Forrest & Einstein, 2001). The mean for fat-free lean mass is 80% as great as the mean for lipid-free soft tissue mass. Thus, the genetic line biases for fat-free lean are greater on a percentage basis than the genetic line biases for fat–free lean mass.

Daily fat–free lean gain on test is estimated as the predicted fat-free lean mass at market weight minus the predicted fat-free lean mass at the beginning of the grow-finish test period divided by the number of days on test. Considering that a 50 lb. pig is predicted to have 17.25 lbs. of fat-free lean (NPB, 2000), the biases for daily fat-free lean gain are greater on a percentage basis than for FFL% at the end of the gain test. The magnitude of the prediction biases of the NPB (2000) equations result in fat-free lean gain values that only predict 15 to 45% of the actual difference in the daily fat-free lean gain and lysine requirements between different genetic populations.

Financial Implications of Using Inaccurate Equations

Current terminal cross pigs are leaner than the line 2 pigs that were used in the lean gain trial. Using the 2000 or 2004 equations results in the under feeding of high lean gain pigs by 3 g of lysine per day. The under feeding of lysine by 3 g per day increases feed to gain by .15 units, increases days to market by 7 d, and reduces plant measured carcass lean percentage by 1% for a total decrease in profitability of $5.40 per pig (De La Llata, Dritz, Tokach, Goodband, & Nelssen, 2007; Schinckel, 2011).

The largest pork producers generally have a Ph.D. nutritionist on staff and conduct large-scale research projects to estimate their pigs' daily lysine requirements for each stage of growth from weaning to market. The largest seedstock companies conduct trials with hundreds of pigs to estimate the lysine requirements for their pigs (De La Llata et al., 2007). However, smaller commercial producers, producers using genetics from small to medium sized independent seedstock suppliers, and youth who are trying to learn about the swine industry rely on Extension swine nutrition guides to estimate their pigs' daily lysine requirements (Von Heugten, 2009). The use of inaccurate prediction of FFL gain and subsequent daily lysine requirements has resulted in these producers being at an economic disadvantage in comparison to other producers (Schinckel, 2011). The current equations do not provide the accurate information needed to implement the genetic, nutritional and management changes needed for commercial producers to remain profitable (Keeler et al., 2007).

Work is being done to produce more accurate equations. Equations were recently developed using fat-free lean data from 203 pigs of seven genetic lines, to predict FFL% from backfat depth and loin depth taken by three different optical probes (Schinckel et al., 2010). The equations included only linear or all significant linear, quadratic, and cross-product variables of backfat and loin depth (Table 2). Plots of the relationships of predicted FFL% to backfat show that the equations were nearly identical for each optical probe and each equation was almost totally linear in nature (Figure 2). The PG- 200 had backfat depths about 0.04 inches greater than the other two optical probes. Pigs measured by the three optical probes have nearly identical estimates of FFL%. Overall, the equations had RSDs of 2.36 to 2.60% and accounted for 72 to 74% of the total variation in FFL%. The correlation of predicted and actual genetic population means were above 0.95 for these equations. The equations predicted over 94% of the actual variation amongst the genetic populations.

Table 2.
Equation for Prediction of Fat-Free Lean Percentage from Optical Probe Measurements or Ribbed Carcass Measurements

		Linear Variables Only					Linear and Quadratic
Eq	Variable	R2	RSD, %	b0	bi	Sign	R2	RSD, %	b0	bi	Sign
1	FD	0.743	2.48	51.2	-12.95	0.001	.770	2.36	60.8	-29.87	0.001
	MD				3.33	0.001				3.23	0.001
	(FD)2									7.09	0.001
2	FD10R	0.785	2.36		-9.58	0.001
	LMA				1.46	0.001
	CW				-0.019	0.034
MD= optical probe muscle depth (in), FD= optical probe fat depth (in), LMA= 10th rib loin eye area (in2), FD10R= off-midline 10th rib fat depth (in), CW= carcass weight from Schinckel et al. 2010.

Figure 2.
Predicted Percent Fat-Free Lean for Three Optical Probes Relative to Backfat Depth

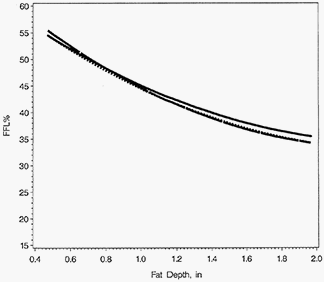
Note: The equations included all significant linear, quadratic and cross-product variables. A 0.30 inch increase in loin muscle depth was predicted for each 1 inch increase in backfat depth.

Impact of Measurement Errors

Prediction equations are calculated by using regression analysis of carcass measurement trials. Consequently, the validity and accuracy of the trials are essential in order to generate accurate equations. Any errors in the trials that the equations are based on will lead to inaccurate equations. Both the magnitude and type of measurement errors affect the absolute value of the regression coefficients and the number of false quadratic, cubic and cross-product variables included in the prediction equations (Schinckel, Einstein, Foster, & Craig, 2007). Different prediction equations that include carcass measurements taken at identical anatomical locations but with different levels and types of measurement errors result in drastically different regression equations with 1) different sets of variables including quadratic, cubic, and cross-product variables and 2) different magnitudes of prediction biases (Schinckel, et al., 2007).

Backfat and loin depth measurements taken at incorrect angles produce measurement errors proportional to the actual value. With such measurement errors, the equations have a high probability of including false quadratic and cross-product variables. As the magnitude of measurement error increases, the accuracy of the equations decrease and the magnitude of genetic population prediction biases increases (Schinckel et al., 2007). In most cases, the lean content of the leanest pigs is under-predicted and the lean content of the fattest pigs is over-predicted.

Conclusions

The accurate estimation of pork carcass composition is essential for all pork producers, independent commercial growers, youth, and seedstock suppliers. The 2000 and 2004 prediction equations for pork carcass leanness are much less accurate than those recently published. Pigs evaluated by different equations may not be assigned the same estimated FFL%. Consequently, the actual differences in carcass lean content between different pigs, or different sets of pigs has been substantially greater than that estimated by the prediction equations in the past decade. Educational efforts to instruct both youth and commercial producers on the differences in pork composition and its relationship to carcass value, nutrient requirements, and profitability have been substantially hindered by the use of inaccurate prediction equations.

The European Community has addressed this issue by the establishment of a requirement that any method used to predict lean yield percentage must have an RSD of 2.5% or less (EC, 1994; Engel, Buist, Fonti, & Lambooiji, 2004). Currently, the United States has not established any requirements relative to the accuracy of the prediction of any measurement of carcass lean percentage. Unfortunately, prediction equations currently being used account for a relatively small percentage of the true variation in pork carcass lean percentage. Published equations are available that are more accurate and less biased that the equations currently being used in the United States (Schinckel et al., 2001, 2010).

The authors and other concerned scientists have recommend that a committee of scientists be formed to develop guidelines for the development of more accurate prediction equations, standards of accuracy and transparency in the reporting of the equations' genetic population, and treatment biases. Prediction equations for pork carcass lean content are so widely used in teaching, research, and Extension that the swine industry needs and deserves the development of accurate standards.

References

Burson, D. (2001). Procedures for estimating pork carcass composition. NPB-AMSA Factsheet. Retrieved from: http://www.extension.org/pages/27311/procedures-for-estimating-pork-carcass-composition

De La Llata, M., Dritz, S. S., Tokach, M. D., Goodband, R. D., & Nelssen, J. L. (2007). Effects of increasing lysine to calorie ratio and added fat for growing-finishing pigs reared in a commercial environment: I. Growth performance and carcass characteristics. The Professional Animal Scientist, 23, 417-428.

Engel, B., Buist W. G., Fonti Furnols, M., & Lambooij, E. (2004). Subpopulations and accuracy of prediction in pig carcass classification. Animal Production, 78, 37-52.

European Community. 1994. EC regulation no. 3127/94, amending regulation (EC) no. 2967/85 Laying down detailed rules for the application of the community scale for grading pig carcasses.

Fortin, A., Tong, A. K. W., & Robertson, W. M. ( 2004). Evaluation of three ultrasound instruments, CVT-2, ultrafom 300 and autofom for predicting salable meat yield and weight of lean in the primals of pork carcasses. Meat Science. 68, 537-549.

Johnson, R. K., Berg, E. P., Goodwin, R., Mabry, J. W., Miller, R. K., Robison, O. W., Sellers, H., & Tokach, M. D. (2004). Evaluation of procedures to predict fat-free lean in swine carcasses. Journal of Animal Science, 82, 2428-2441.

Keeler, G. L., Tokach, M. D., Goodband, R. D. , Nelssen, J. L., & Langemeier, M. R. (1994). Assisting swine producers to maximize marketing returns. Journal of Extension [On-Line], 32(1) Article 1FEA7. Available at: https://www.joe.org/joe/1994june/a7.php

Nash, S. A. (2007). Ultrasound technology helps youth raise industry-acceptable market animals. Journal of Extension [On-Line], 45(4) Article 4RIB4. Available at: https://www.joe.org/joe/2007august/rb4.php

NPB. (1999). Fat-free lean prediction equations. 1999 Results. National Pork Board, Des Moines, Iowa.

NPB. (2000). Pork composition and quality assessment procedures. National Pork Board, Des Moines, Iowa.

National Research Council (NRC). (1998). Nutrient requirements of swine, 10^th revised edition. National Academic Press, Washington, DC.

Pomar, C., Marcoux, M., Gispert, M., Fonti Furnols, M., & Daumas G. (2008). Determining the lean content of pork carcasses. In: J. D. Kerry, D. P. Ledward, & D. Ledward (Eds.) Improving the sensory and nutritional quality of fresh meat ( 493-518). Woodhead Publishing Limited, Cambridge, UK.

Rusk, C. P., Martin, C. A., Talbert, B. A., & Baischweid, M. A. (2002). Attributes of Indiana's 4-H livestock judging program. Journal of Extension. [On-Line], 40(2) Article 2RIB5. Available at: https://www.joe.org/joe/2002april/rb5.php

Schinckel, A. P., & de Lange C. F. (1996). Characterization of growth parameters needed as inputs for pig growth models. Journal of Animal Science, 74, 2021-2036.

Schinckel, A. P., Wagner, J. R., Forrest J. C., & Einstein M. E. (2001). Evaluation of alternative measures of pork carcass composition. Journal of Animal Science, 79, 1093-1119.

Schinckel, A. P., Einstein, M. E., Foster, K., & Craig, B. A. (2007). Evaluation of the impact of errors in the measurement of backfat depth on the prediction of fat-free lean mass. Journal of Animal Science, 85, 2031- 2042.

Schinckel, A. P., Wagner, J. R., Forrest J. C., & Einstein M. E. (2010). Evaluation of the prediction of alternative measures of pork carcass composition by three optical probes. Journal of Animal Science, 88, 767-794.

Schinckel, A. P. (2011). The cost of inaccurate prediction of fat-free lean gain in pigs. Feedstuffs. March 28, 2011. pp 8-9.

Von Heugten, E. ( 2009). Growing-finishing swine nutrient recommendations and Feeding management. National Swine Nutrition Guide. Retrieved from: http://www.usporkcenter.org/UserFiles/file/NSNG/NSNG-Growing-Finishing%20Nutrient%20Recommendations(1).pdf