Education and Persuasion in Extension Forestry: Effects of Different Numerical Information Formats

Introduction

Extension work involves a great deal of communication across a number of different parties: Farmers and ranchers, researchers, corporations, government agencies, the general public, and others. Effective communication--being both informative and persuasive--is hard to achieve across so many audiences, especially when trying to communicate complex issues (e.g., issues that often include numerical and statistical information). It is therefore relevant to Extension work to ask how we can best communicate such numerical information. This article uses recent findings from experimental psychology on how people perceive numerical information, and applies those findings to a test case in Extension work: Forestry Extension in Missouri.

Missouri is often cited as a microcosm of national demographics and trends (Robertson, 2004; Gardner, 2004). This is certainly true in the case of family-owned forestland, particularly in relation to the eastern United States (Butler & Leatherberry, 2004). According to the 2004 U.S. Forest Service's National Woodland Owner Survey, there are over 350,000 family-owned forests in Missouri. Collectively, these private citizens own approximately 83% of the state's 14 million acres of forestland. While, on an area basis, the number of family forests less than 100 acre equals the number of forested parcels greater than 100 acres, the number of landowners (329,000) disproportionately lies in the former group. Further, less than 10% of these landowners have a management plan or have sought professional help in managing their natural resources.

Proper management of these family-owned forests is vital for sustaining the country's natural resources and high quality of life. These forest resources provide for viable ecosystems that support biological diversity and wildlife habitat. Woodland ecosystems contribute significantly to local economies; are fundamental elements of urban and rural communities; and are integral to the quality of life for all the citizens of the country.

Everyone expects a safe and healthy environment and an agricultural and forestry industry that serve as stewards of the natural resource base. But how do we increase the number of private landowners practicing good forest stewardship? Forestry Extension has at least two fundamental goals:

• Develop and foster an awareness of the important role family-owned forests play in our nation's land legacy,


• Encourage active stewardship of these forest resources.

These purposes are mutually consistent so long as a better understanding of the state of forestry promotes responsible forest stewardship.

The Psychology of Understanding and Persuasion

In this respect, the psychological study of persuasion is of vital interest to those in the Forestry Extension area; how does one persuade people to donate their time and money to forest stewardship issues? While the majority of research in persuasion has focused on behavioral tactics and methods of deploying information in attempts to persuade (e.g., Cialdini, 2001; Petty, Wegener, & Fabrigar, 1997), the persuasive impact of statistical information, as presented in different types of formats has been touched on by only a few studies (Brown & Newman, 1982; Halpern, Blackman, & Salzman, 1989). Statistical information, though, is often at the heart of persuasive messages; for instance, how effective do you think the numerical information was in the first paragraph of this article?

Recent research on human judgment and decision-making abilities hold important implications for how different statistical formats are perceived and used in cognitive processes (e.g., Brase, 2002a, 2002b; Brase, Cosmides, & Tooby, 1998; Gigerenzer & Hoffrage, 1995; Hoffrage, Lindsey, Hertwig, & Gigerenzer, 2000). This research has proposed that the human mind was designed by evolutionary history to most effectively acquire and use information in the format of natural frequencies, that is, information about the frequencies of objects, events, and locations as they are encountered and recognized in the world (e.g., Out of 100 trees, 25 have fruit. And of those 25 with fruit, 20 are edible right now). Such information not only is ecologically valid in terms of source, but has advantages over other formats in terms of flexibility and computational ease (Gigerenzer & Hoffrage, 1995). These properties suggest that frequencies can help generate better understanding of messages and thereby more persuasive messages. (See Table 1 for a summary of different numerical formats.)

Table 1.
Examples and Key Properties of Different Numerical Formats (Using Missouri Forestry Information as Examples)

Format	Example	Properties
Absolute Frequencies	350,000 family-owned forests in Missouri	Raw (non-standardized) counts of frequencies, often non-quantitative reference class
Simple Frequencies	1 out of every 10 small family forests have a management plan	Frequency counts, reduced to smallest ratio with reference class
Relative Frequencies	Private citizens own 83% of Missouri's forest land	Frequencies standardized to a reference class of 100 (occasionally confidence statements)
Single-Event Probabilities	There is a 0.83 probability that a piece of forest is privately owned.	Likelihood statements (can be frequency or personal confidence) standardized to a reference class of 0-1
Natural Frequencies	11.6 million out of 14 million acres of forestland are privately owned; 5.8 out of those 11.6 million acres are parcels less than 100 acres.	Absolute/simple frequencies in a natural sampling (subset) framework

Other research in the field of judgments under uncertainty has documented that when people are asked to make decisions about smaller groups (e.g., family or small-group populations under 100 people), some of the traditionally observed judgment errors significantly lessen or disappear (Tversky & Kahneman, 1981; Wang, 1996a, 1996b; Wang & Johnson, 1995). The explanation for this improvement stems from the rationale that these smaller population sizes are on scales of magnitude with which humans have directly and recurrently dealt over their evolutionary history.

What is important for the present purposes is that this view suggests absolute frequency information about very large reference classes (for example, 1,100,000 people visit a national park each day during peak summer months) is not perceived on a normal numerical scale, but rather in a logarithmic manner similar to the changes in difference thresholds in sensory perception (Cohen & Ward, 1989). In other words, as numbers get very large, it takes proportionately bigger differences for people to notice that a difference exists.

Brase (2002a) found that very large reference classes (i.e., the U.S. population of 280 million) can indeed lead to systematic distortions in the persuasive impact on both attitudes and potential behaviors (i.e., social influence). Specifically, proportionally small populations expressed as an absolute frequency of a large reference class (e.g., "2.8 million Americans will be exposed to the flu") had more influence on decisions than the same information in different formats (e.g., "1% of Americans will be exposed to the flu") and were seen as representing more significant issues.

At the same time, proportionally large populations expressed as a absolute frequency of a large reference class (e.g., "a drug has be estimated to be effective for 272 million Americans"), had less influence on decisions than the same information in different formats (e.g., "a drug has be estimated to be effective for 99% of Americans") and were seen as representing less significant issues. Both this and the previous research by Wang and colleagues have all been based on hypothetical situations that happen to be amenable to laboratory settings. The basic logic of the research by Brase (2002a), however, can be applied to specifically selected topics.

The objective of the study reported here was to extend the prior laboratory findings on the effects of numerical formats (absolute frequencies, relative frequencies [percentages], and simplified frequencies) in a specific, more applied, context. This parallels aspects of earlier laboratory research (Brase, 2002a). Two patterns were predicted: 1) Absolute frequencies will generally be perceived as greater quantities than the other format, particularly for small proportions of large reference classes, and 2) Both percentages (relative frequencies) and simplified frequencies will generally be perceived as clearer and easier to understand than absolute frequencies (so long as the reference class is very large).

Experiment 1

Participants

Participants were 96 undergraduates at a public research university in the Midwestern U.S., who participated as partial fulfillment of a course requirement. The average age of the participants was 18.9 years.

Materials and Procedure

Each participant was given a one-sheet survey that consisted of brief instructions followed by the actual study materials. The materials consisted of five pairs of statistical information, each of contrasting numerical formats (simple frequencies versus total frequencies, or relative frequencies [percentages] versus total frequencies); simple frequencies were not contrasted with relative frequencies (e.g., 3 out of 4 versus 75%) because these numbers are fairly easily understood as equivalent).

The numerical information was all about forestry-related issues, expressed in terms of statewide resources. (See Appendix for statements.) The reference for all the data was the state of Missouri, with other state names inserted to give the appearance of two separate pieces of information (other states were selected to be as close as possible to Missouri in terms of size, population, or economy, as appropriate for the information statement). Each participant received one of two intermixed combinations of simple frequency/total frequency comparisons and relative frequency/total frequency comparisons. The presentation of the different numerical formats (first or second) was also randomly varied.

Each pair of numerical statements was followed by two probe questions that asked participants to evaluate the greater clarity and the greater quantity of the two numerical statements. Specifically, the first question asked, "Which of the above statements gives you the clearest understanding of the situation for that state?," and the second question asked which state had the largest or most of the item quantified in the statements (i.e., privately owned forest land, non-farm non-residence family-owned forests, family forests using management plans or professional advice, proportion of the state's gross product from the forest products industry, and employees in forestry-based industries). There was no time limit for completing the study, and all participants finished within 15 minutes.

Results

The proportions of participants selecting one numerical statement over another are presented in Figures 1a and 1b (for nominations of greater clarity) and in Figures 2a and 2b (for nominations of greater size). Nonparametric binomial tests were used to identify response patterns that were significantly different from indifference (0.50). Findings of statistically significant differences are indicated in the figures.

The ratings of clarity show that, overall, percentages and simple frequencies are consistently perceived as clearer and more understandable than absolute frequencies. The patterns across the different items further suggest some finer distinctions, although these are much more tentative. Percentages appear to be particularly clear at extremes and with very large quantities. Simple frequencies, on the other hand, appear to be particularly clear for intermediate amounts and small absolute quantities.

Figure 1a and 1b.
Experiment 1 Ratings of Clarity, Comparing Absolute Frequencies (E.G., 10 Million) with Percentages (E.G., 75%) and Comparing Absolute Frequencies with Simple Frequencies (e.g., 3 out of 4)




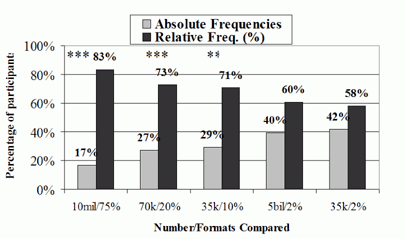
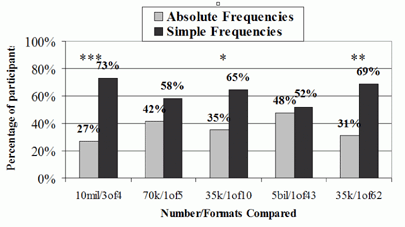
For all Figures, statistical significance test results are shown using the following notations: "*"= p<0.05, "**"=p<0.01, and "***"=p<.001.

The ratings of how large quantities are show that, overall, absolute frequencies are almost always perceived as larger amounts (a particularly remarkable finding, given that the quantities were basically equivalent). The patterns across the different items again suggest some finer distinctions that can be cautiously advanced. Small percentages seem to be perceived as lesser quantities than equivalent absolute frequencies, but large percentages apparently can be perceived as a quantity on par with absolute frequencies.

Figures 2a and 2b.
Experiment 1 Ratings of Greater Value, Comparing Absolute Frequencies (E.G., 10 Million) with Percentages (E.G., 75%) and Comparing Absolute Frequencies with Simple Frequencies (e.g., 3 out of 4)

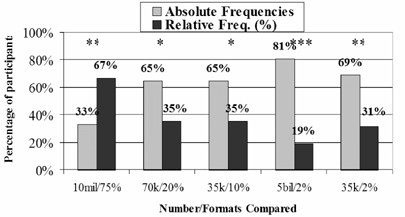
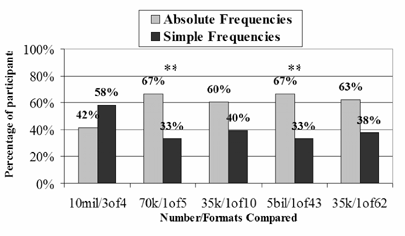
Experiment 2

A chronic concern in many behavioral research areas, but in particular areas that propose to be studying the general public, is the representativeness of college undergraduates as subjects. To address this concern we collected further data, but using participants who were more representative of general population members who might be expected to encounter and evaluate forestry information.

Participants

Participants were 69 adults who participated either during a woodland steward university short course (n=32) or during a conference on tree management (n=37). All participated voluntarily, and the average age of the participants was 57.5 years (range: 27-83).

Materials and Procedure

Each participant was given the same sheet survey, following the same procedure, as in Experiment 1.

Results

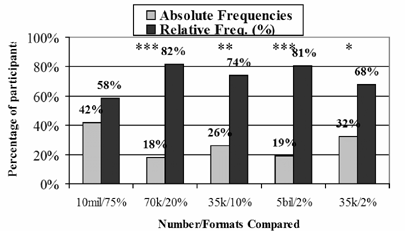
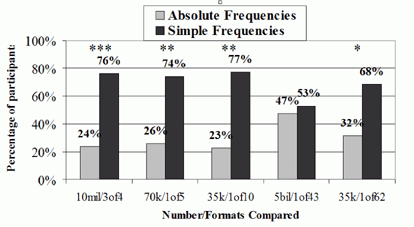
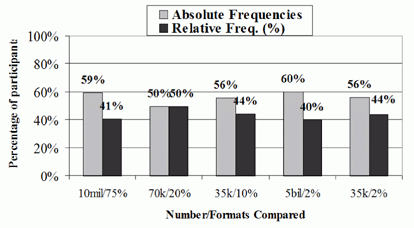
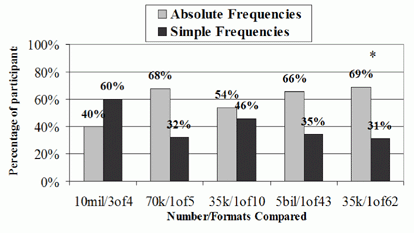
The proportions of participants selecting one numerical statement over another are presented in Figures 3a and 3b (for nominations of greater clarity) and in Figures 4a and 4b (for nominations of greater size). Nonparametric binomial tests were again used, and findings of statistically significant differences are indicated in the figures. The results were broadly similar to the results of Experiment 1:

• Relative frequencies and simple frequencies were consistently rated as clearer than absolute frequencies, across all items.


• Under most circumstances, absolute frequencies were again perceived as greater quantities than mathematically equivalent statements expressed in relative frequencies or simple frequencies
  • As in Experiment 1, normalized frequencies for large proportions of a reference class (e.g., 3 out of 4) are the only contexts that are perceived to be as large as equivalent absolute frequencies

  • The greater magnitude perception for absolute frequencies was less pronounced than in Experiment 1.

It is also noteworthy that a number of participants, unlike in Experiment 1, refused to judge which quantity of the pairs was greater, arguing (correctly, in fact) that they would need the reference classes for the absolute frequencies in order to make an accurate evaluation.

Figures 3a and 3b.
Experiment 2 Ratings of Clarity, Comparing Absolute Frequencies (E.G., 10 Million) with Percentages (E.G., 75%) and Comparing Absolute Frequencies with Simple Frequencies (e.g., 3 out of 4)

Figures 4a and 4b.
Experiment 2 Ratings of Greater Value, Comparing Absolute Frequencies (E.G., 10 Million) with Percentages (E.G., 75%) and Comparing Absolute Frequencies with Simple Frequencies (e.g., 3 out of 4)

Discussion

Two studies, using both university undergraduates and members of the general population, found that:

• Percentages (relative frequencies) and simple frequencies are perceived as clearer and easier to understand than absolute frequencies and


• Across a range of values that express fairly small proportions of a class, absolute frequencies were perceived as greater in magnitude than mathematically equivalent percentages or simple frequencies.

What does this mean for forestry outreach? Much of the information disseminated in the process of working with communities is quantitative information; how much land, how many dollars, how many trees, etc. The format of that information can be chosen to better accomplish particular forestry outreach goals:

• One should consider using absolute frequencies when the goals are to get people's attention, to persuade people, or to emphasize the magnitude of an issue. For example, the fact that there are over 350,000 family-owned forests in Missouri is impressive and can garner attention (even though it is a small proportion of the state population of about 5.8 million people).


• One should consider using relative and simple frequencies when the goals are to help people understand, accurately compare, or clarify issues. For example, "less than 10%" is easier to understand compared to "less than 33,000 of the 329,000 Missouri family forests smaller than 100 acres have a management plan."

What about situations in which there are mixed goals; when one wants to both educate and persuade? The best strategy would appear to be a dual presentation: present information in both relative (or simple) frequencies and absolute frequencies. This approach requires more time and audience attention, as one might anticipate given the premise that two goals are being pursued. The better Extension professionals understand the various ways individuals perceive statistical information, the more effective they can be in connecting with their clients.

References

Brase, G. L. (2002a). Which statistical formats facilitate what decisions? The perception and influence of different statistical information formats. Journal of Behavioral Decision Making, 15(5), 381-401.

Brase, G. L. (2002b). Ecological and evolutionary validity: Comments on Johnson-Laird, Legrenzi, Girotto, Legrenzi, & Caverni's (1999) mental model theory of extensional reasoning. Psychological Review, 109(4), 722-728.

Brase, G. L., Cosmides, L., & Tooby, J. (1998). Individuation, counting, and statistical inference: The roles of frequency and whole object representations in judgments under uncertainty. Journal of Experimental Psychology: General, 127, 3-21.

Brown R. D., & Newman D. L. (1982). An investigation of the effect of different data presentation formats and order of arguments in a simulated adversary evaluation. Educational Evaluation & Policy Analysis, 4, 197-203.

Butler, B. J., & Leatherberry, E. C. (2004). America's family forest owners. Journal of Forestry, 102:7, 4-9.

Chaiken, S., & Trope, Y. (Eds.) 1999). Dual-process theories in social psychology. New York: Guilford.

Cialdini, R. B. (2001). Influence: Science and practice. Boston, MA: Allyn and Bacon.

Cohen, S., & Ward, L. M. (1989). Sensation & perception, 3^rd edition. San Diego, CA: Harcourt Brace Jovanovich, Publishers.

Gardner, J. (2004). Constantly seeking relevancy. Synthesis 3:4, 1-2.

Gigerenzer, G., & Hoffrage, U. (1995). How to improve Bayesian reasoning without instruction: Frequency formats. Psychological Review, 102, 684-704.

Halpern, D. F., Blackman, S., & Salzman B. (1989). Using statistical risk information to assess oral contraceptive safety. Applied Cognitive Psychology, 3, 251-260.

Hoffrage, U., Lindsey, S., Hertwig, R., & Gigerenzer, G. (2000). Medicine--Communicating statistical information. Science, 290, 2261-2262.

Levine, R. L., Martinez, T. S., Brase, G., & Sorrensen, K. (1994). Helping behavior in 36 cities across the United States. Journal of Personality and Social Psychology, 67, 69-82.

Petty, R. E., Wegener, D. T., & Fabrigar, L. R. (1997). Attitudes and attitude change. Annual Review of Psychology, 48, 609-647.

Robertson, D. B. (2004) Bellweather politics in Missouri. The Forum: 2:3, Article 2.

Smith, E. R., & DeCoster, J. (2000). Dual process models in social and cognitive psychology. Personality and Social Psychology Review, 4, 108-131.

Tversky, A., & Kahneman, D. (1981). The framing of decisions and the psychology of choice. Science, 211, 453-458.

Wang, X. T. (1996a). Domain-specific rationality in human choices: Violations of utility axioms and social contexts. Cognition, 60, 31-63.

Wang, X. T. (1996b). Framing effects: Dynamics and task domains. Organizational Behavior & Human Decision Processes, 68, 145-157.

Wang, X. T., & Johnston, V.S. (1995). Perceived social context and risk preference: A re-examination of framing effects in a life-death decision problem. Journal of Behavioral Decision Making, 8, 279-293.

Appendix

Instructions: Answer the questions about each set of statements, using the letters before each statement. There are no requirements that you use all the statements (that is, you may decide that a particular statement is the answer for more than one question). Please answer with your best judgment, even if you are not sure of the correct answer.

• 10.5 million acres of Missouri's forest land are owned by private citizens.
• 75% of North Dakota's forest land is owned by private citizens.
• 3 out of every 4 acres of Wisconsin's forest land are owned by private citizens.


• 70,000 of the family-owned forests in Missouri are not part of a farm or the owner's primary residence.
• 20% of the family-owned forests in Wisconsin are not part of a farm or the owner's primary residence.
• 1 out of 5 of the family-owned forests in North Dakota are not part of a farm or the owner's primary residence.


• 35,000 of the privately held family forests in North Dakota have a management plan or have sought professional advice.

• 10% of the privately held family forests in Wisconsin have a management plan or have sought professional advice.

• 1 out of 10 of the privately held family forests in Missouri have a management plan or have sought professional advice.


• The forest products industry constitutes $4.7 billion dollars of Colorado's Gross State Product.
• The forest products industry constitutes 2.3% of Missouri's Gross State Product.
• The forest products industry constitutes 1 of every 43 dollars of Wisconsin's Gross State Product.


• 34,600 employees in Missouri work in forestry-based industries.
• 1.6% of employees in Tennessee work in forestry-based industries.
• 1 out of every 62 employees in Wisconsin work in forestry-based industries.

[Both forms included the absolute frequency statements, which were compared with the percentages and simple frequencies that are underlined (Form A) or that are italicized (Form B).]